About Thinking Strategies
Development
In her work with students, Celia was surprised that several of her high school students did not know their basic facts, especially multiplication. She found that providing them strategies helped them, so she started creating her own strategies. She also would pair similar facts together and teach the easier facts first instead of teaching the facts in sequential order.
She soon realized there was a need for a resource that would provide teachers an efficient and effective way to teach basic facts. Using John Van de Walle's approach, coupled with her experience and puzzle-making ability, she developed her first basic facts resource in 2002, called Times for Times. She presented it soon after at the Manitoba Teachers convention and was astounded by the response and interest. Teachers asked her to make resources for the other operations. The complete Thinking Strategies series was published by Portage and Main press in 2006.
Portage and Main Press continued to publish the resource until 2016. At that point, they returned the rights to Thinking Strategies back to Celia's children. Celia's children have now proudly published the Thinking Strategies series under MathImagine, Celia Baron's original company.
How It Works
Providing an Intuitive Step-wise Approach
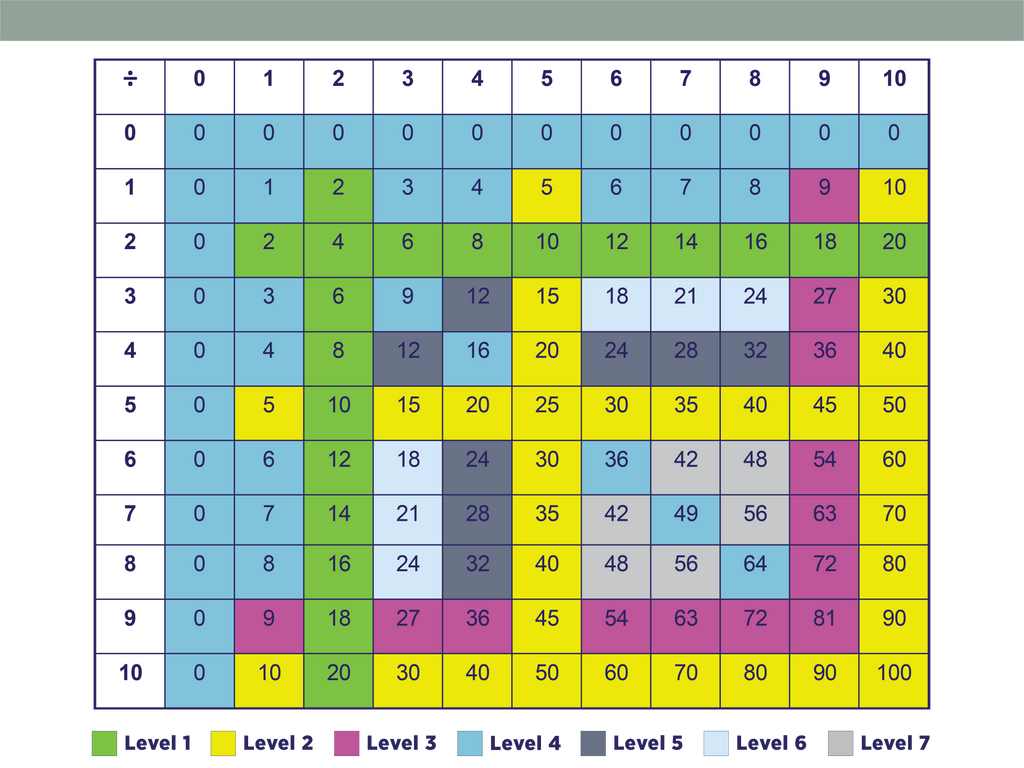
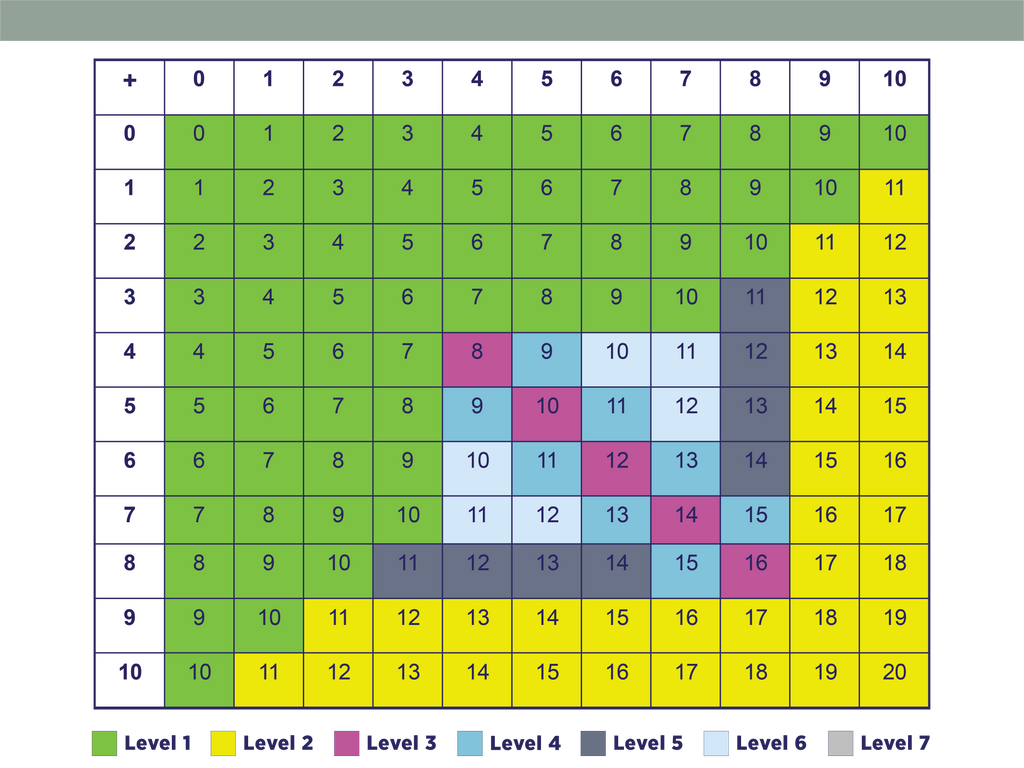
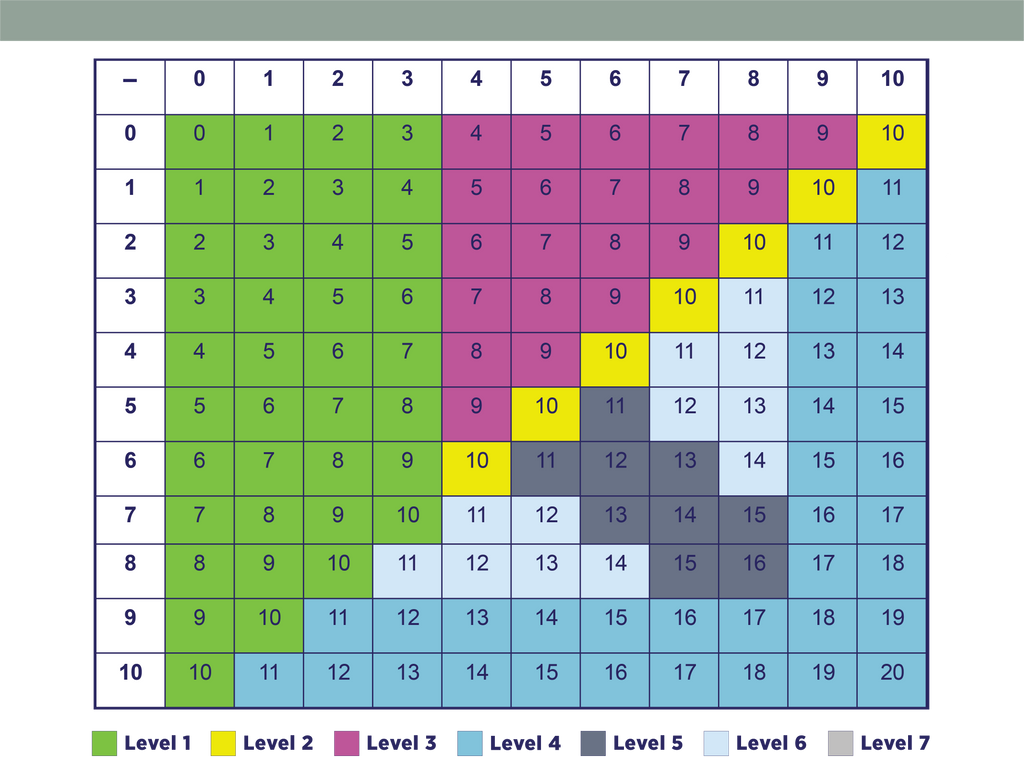
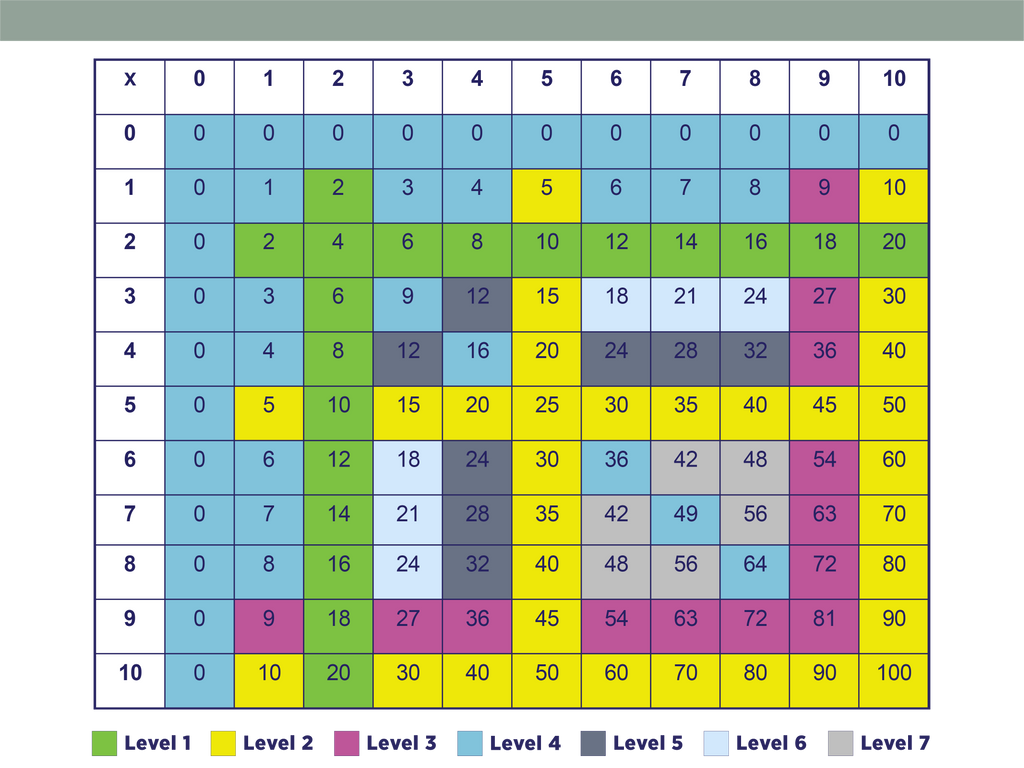
The Thinking Strategies series chunks related facts together and introduces these chunks progressively to allow students to learn basic facts easily and efficiently. See the grids on bottom of the page for the chunking and ordering we use.
Using Thinking Strategies to Reach Fluency
The theory behind using a thinking strategy is based on the work of John Van de Walle. A thinking strategy is a tool that helps complete facts quickly. For a strategy to be a thinking strategy, it must be done mentally and it must be efficient. Some strategies are visual (for example, a clock, which is used to complete facts with a factor of five). Other strategies are auditory and involve silly sayings or rhymes, while others involve pattern recognition.
Many thinking strategies are provided for each fact and often include models. Students are encouraged to use as many strategies as possible to complete the facts. The resource also encourages translation from one mathematical language to another.
Practice, Practice, and More Practice
To build fluency, students need to practice the facts. The series provides this in abundance with lesson plans full of ideas for activities, engaging student activity sheets, and extra group activities. Accessory resources are available for additional practice opportunities.
John Van de Walle's Approach
John Van de Walle felt that all students are able to "master" basic facts if they follow three steps:
1. Develop a strong understanding of the operations and number relationships.
2. Develop efficient thinking strategies for fact retrieval.
3. Practice the use and selection of those strategies.
He defined "mastery" as a quick response time of less than 3 seconds, without using inefficient means such as counting. In later editions of his work, the terminology was changed from "mastery" to "fluency" but the concept remains the same.
Elementary and Middle School Mathematics: Teaching Developmentally (5th edition). John A. Van de Walle. Allyn & Bacon 2003.
Celia's steps to fluency
Celia outlined the following sequence of steps that students typically follow as they progress toward John Van de Walle's concept of fluency. These steps provide teachers with a clear way to understand where students' are in the learning process.
Stage 1: Incorrect response/an inappropriate thinking strategy
Stage 2: Correct response in more than three seconds using an appropriate thinking strategy
Stage 3: Correct response within three seconds using an appropriate thinking strategy
Stage 4: Correct response that is automatic and occurs without thinking
Chunks for Each Operation
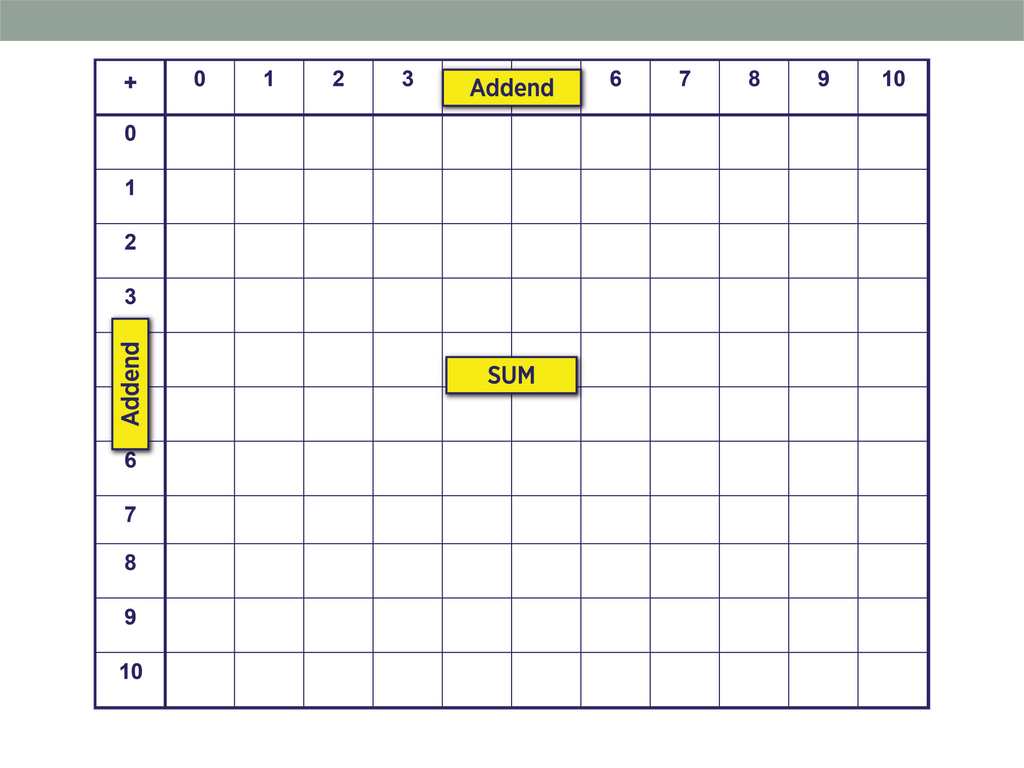
Addition
Subtraction
Multiplication
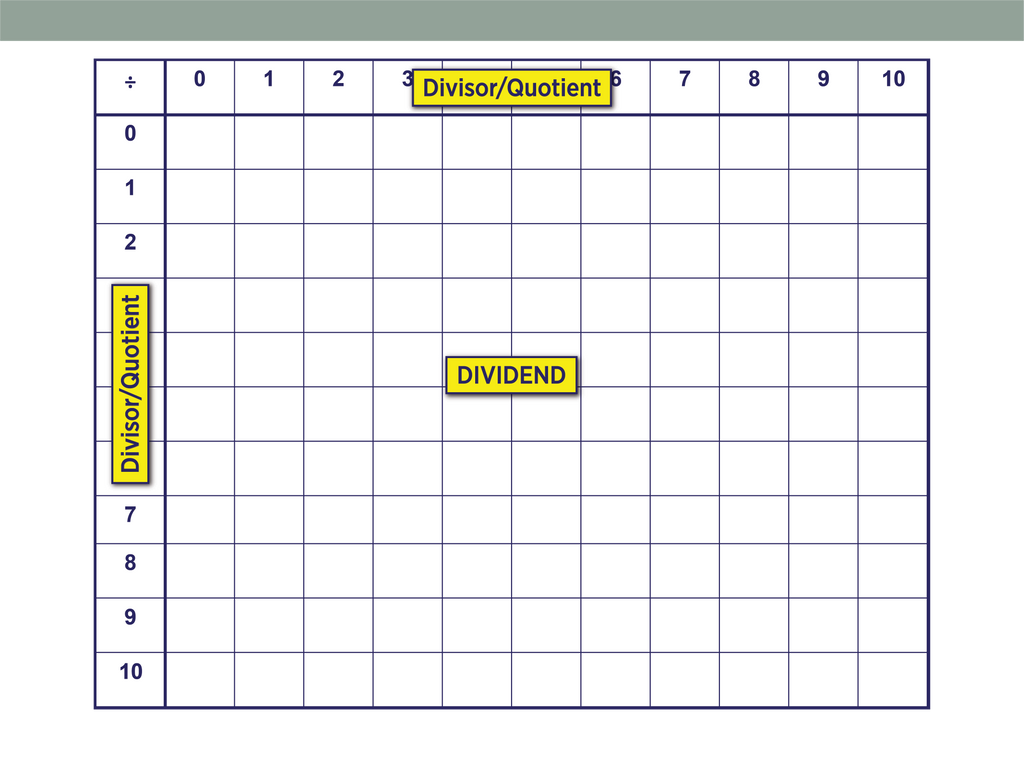
Division